고정 헤더 영역
상세 컨텐츠
본문

지난 시간까지는 (자연수)가 포함된 분수의 곱셈을 하였습니다. (분수) × (자연수), (자연수) × (분수)를 해결하며 원리를 찾아보았습니다. 이번 시간에는 (분수) × (분수) 인 분수의 곱셈 최종 단계를 함께 해결해보고자 합니다.
1. (분수)×(분수)의 계산 원리 알아보기
이번 시간에는 문제를 먼저 제시하고 않고 식을 먼저 제시하였습니다. 오늘은 (분수) × (분수)의 원리 찾는데 집중하는게 더 중요하다는 생각이 들었기 때문입니다.

아이들에게 1학기에 분수의 덧셈할 때 활용했던 투명분수판을 아이들에게 제시하고 투명분수판으로 문제를 해결해자고 하였습니다. 많이 어려운 경우 분수 그림이나 글로 설명해보도록 하였습니다.
2. 투명 분수판
저는 쉽고 당연하게 생각했는데 아이들은 어렵게 생각하였습니다. 역시 문제만 풀 수 있다고 아는게 아니라는 것을 다시 한 번 느꼈습니다. 이전의 경험을 통해 둘을 겹친다고는 생각을 하였는데, 겹쳐서 어떻게 나타내야 하는지에 대해 쉽게 생각해 내지 못했습니다.
크게 세 무리로 나뉘었습니다. 극 소수지만 아예 분수의 덧셈으로 해결하는 아이들이 있었습니다. 예전에 배웠던 기억을 더듬어 아예 분수의 덧셈으로 문제를 해결하였습니다. 확실하게 원리를 정리하지 않으면 이렇게 새로운 내용을 배우게 될때 헷갈리게 됩니다. 그래서 분수의 곱셈과 덧셈을 비교할 필요가 있다는 생각이 들었습니다.
또 한 무리는 색깔이 겹쳐지는 부분이 분자가 되는 것은 알겠는데, 왜 이게 분자가 되는지 설명을 못하는 아이들입니다. 이 아이들의 경우는 문제를 해결하는 방법은 아는데 왜 그런지에 대한 고민 없이 방법만 알고 있는 아이들일 확률이 높습니다.
마지막 무리는 정확하게 내용을 알고 그 원리에 따라 문제를 해결하는 아이들입니다.
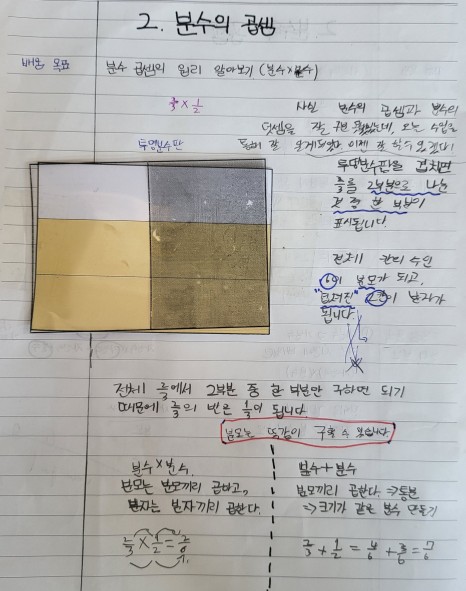
바로 아이들의 설명을 듣기보다 모둠에서 설명을 하고 궁금한 점을 나누는게 더 도움이 될 것이라고 생각이 들어 모둠별로 자신의 해결 방법을 발표하도록 하였습니다. 모둠에서 설명을 듣고서야 이해하는 아이들이 많았습니다. 그런 다음 전체적으로 각 방법 별로 발표를 하고 설명을 들어보았습니다. 투명 분수판을 겹치면 나뉘어지는 칸의 수가 (분모)로, 색깔이 겹치는 부분의 수가 (분자)로 됨을 알 수 있습니다.
× (1/2)이라는 것은 2개로 묶은 부분 중 한 부분이라는 의미를 활용해서 설명을 하였습니다.
아이들이 어려워한 부분은 왜 색깔이 겹치는 부분이 분자가 될까였습니다. 이 부분에 대해 생각을 해보지 않아서 인지 "그런 것 같긴한데, 왜 그러지?"라는 생각을 하는 것 같았습니다. 색칠이 되어 있어서 헷갈릴 수 있는데 실은 1/2배 한다는 것은 2개 중의 한 부분이고, 이는 2/3을 반으로 나눈 것 중 한 부분입니다. 노란색 색칠 된 것이 2/3이고, 그중 반이 × 1/2을 의미하므로 겹쳐진 부분만 분자로 봐야 하는 것입니다.
3. 분수 그림
아이가 ×1/2의 설명을 정확하게 잘 활용해서 설명하였습니다. 2/3를 2 부분으로 나누면 1/3인데, 그 중 한 부분만 구하면되니 1/3이라고 했습니다. 아주 정확하게 잘 이해하고 있었습니다.
4. 글로 설명
이 아이도 이전에 배웠던 분수 곱셈의 의미를 잘 이해하고 있기 때문에 글로 정확하게 잘 풀어서 설명을 하였습니다.
5. 분수의 덧셈과 곱셈의 비교

그리고 나서 원리를 정리하면서 오늘은 1학기 때 배운 분수의 덧셈과 지금 배우는 분수의 곱셈이 어떻게 다른 것인지를 한 번 살펴보도록 하였습니다. 우리가 분수의 덧셈을 해결할 때도, 분수의 곱셈을 해결할 때도 투명 분수판을 사용했는데 그 의미나 결과가 어떻게 다른지 살펴보았습니다.
아이들은 공통점으로 분모를 바로 구할 수 있다는 점을 찾아주었습니다. 그러나 그 의미가 분수 곱셈은 곱하는 분수의 분모만큼 묶는다는 의미를 가지고 분수의 덧셈은 통분의 의미를 가지기 때문에 다르다는 것을 확인하였습니다. 그래서 당연히 결과도 달라짐을 확인하였습니다.
6. 학생들 공책 정리



'초등 5학년 수학' 카테고리의 다른 글
| 2. 분수의 곱셈, 단원 성취기준 도달 확인 평가(5학년 2학기) (3) | 2024.04.17 |
|---|---|
| 2. 분수의 곱셈, 통합적 이해, 곱셈 원리를 하나로 정리(5학년 2학기) (4) | 2024.04.16 |
| 2. 분수의 곱셈, (자연수)×(대분수) 해결 원리 탐구하기(5학년 2학기) (4) | 2024.04.14 |
| 2. 분수의 곱셈, 분수의 곱셈 원리 이해하기(5학년 2학기) (4) | 2024.04.13 |
| 2. 분수의 곱셈, (대분수)×(자연수)의 원리 탐구하기(5학년 2학기) (3) | 2024.04.11 |




