고정 헤더 영역
상세 컨텐츠
본문

지난 시간까지 궁금증을 통해 분수의 나눗셈 탐구 질문을 찾아보고, 분수 및 나눗셈에 대한 내용에 대해 복습을 하였습니다. 이번 시간에는 (자연수) ÷ (자연수) 원리에 대해 알아보는 시간을 가졌습니다.
1. (자연수)÷(자연수) 원리 개별 탐구하기
4인분의 볶음밥 재료를 제시하고 1인분의 양을 구하는 것으로 문제 상황을 제시하였습니다.

이번 시간에는 자연수 끼리의 나눗셈을 다루기 때문에 감자와 파, 버섯의 1인분 양을 구해보도록 하였습니다. 나눗셈 문제에서 늘 시각화를 강조하기 위해 그림으로 문제를 해결해보도록 하였습니다.
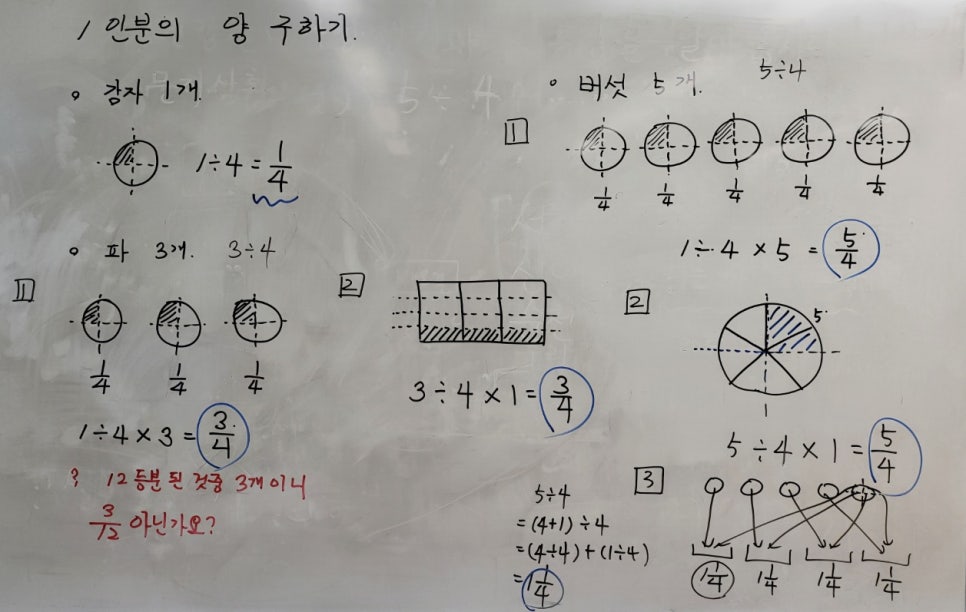
감자 1인분 양 구하기
4인분에 필요한 감자 1개의 1인분 양을 구하기 위해서는 1을 4로 나누어 1/4을 구하였습니다. 이는 대부분의 아이들이 똑같이 그렸기 때문에 금방 확인할 수 있었습니다.
파 1인분 양 구하기
4인분에 필요한 파 3개의 1인분의 양을 구하기 위해서는 3을 4로 나누는 과정을 그림으로 표현해보도록 하였습니다. 이는 두가지 방법으로 나뉘었습니다. 파 1개씩 4등분해서 1/4이 3개이기 때문에 3/4으로 구한 경우와 전체를 4개로 나누어 구한 경우였습니다.
이때 그림으로 보면 3/4이 아닌 12등분 된 것 중 3개로 보이니 3/12아닌가?에 대해 질문을 하였습니다. 아이들은 갑자기 당황하기 시작했습니다. 분수는 전체와 부분의 의미가 중요한데, 전체를 무엇으로 보느냐에 따라 의미가 달라질 수 있기 때문에 자신이 어떻게 그렸는지를 잘 확인하며 나눗셈을 보도록 하였습니다.
1개를 4부분으로 나눌 때는 전체를 1로 보았을 때고 그럼 1을 4로 나누게 되고 그것이 3개 있는 것이 됨을 확인했습니다. 그리고 3을 전체로 보았을 때는 3 자체를 4로 나누게 됨을 아이들과 이야기 나누며 확인하였습니다.
버섯 1인분 양 구하기
4인분에 필요한 버섯 5개의 1인분 양을 구하기 위해서는 5를 4로 나누는 과정을 그림으로 표현하도록 하였습니다. 이는 세가지 방법으로 나뉘었는데, 그 과정은 아이들이 해결한 과정으로 대체하겠습니다.
첫번째는 등분제 나눗셈처럼 하나씩 나눈 다음 남는 부분만 똑같이 나눈 경우입니다.
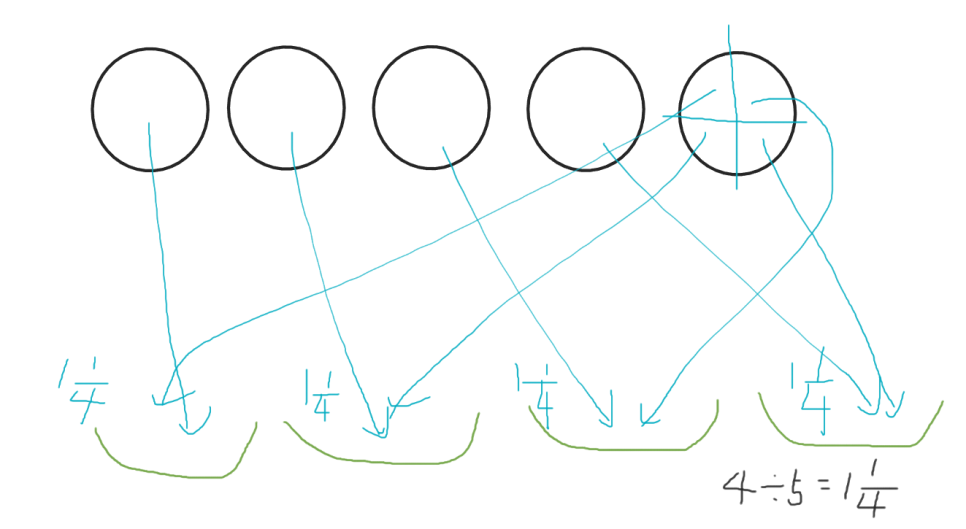
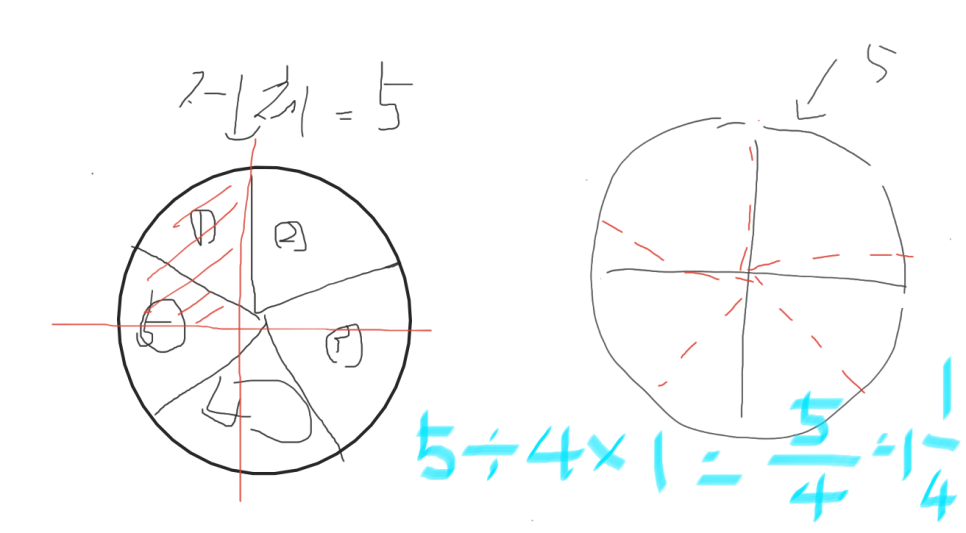
두번째는 전체 5를 4등분하여 1부분의 크기를 구하는 방법입니다.
세번째는 대부분의 아이들이 활용하는 방법으로 1을 전체로 보고 이를 4등분 한 뒤 그 개수를 곱하는 방법입니다.
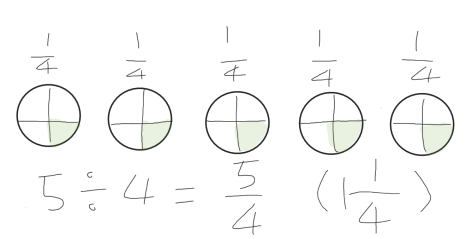
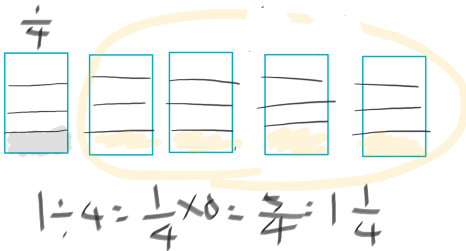

어떻게 해결을 하든 그 결과는 같게 나옴을 확인하고 문제를 해결하는 과정이 조금씩 다르고 그 과정에 대한 의미도 각각 다르니 이를 파악하면서 나눗셈 활동에 참여할 수 있도록 하였습니다.
2. 모둠 토의를 통한 (자연수)÷(자연수) 원리 발견하기
어떻게 해결을 하든 그 결과는 같게 나옴을 확인하고 문제를 해결하는 과정이 조금씩 다르고 그 과정에 대한 의미도 각각 다르니 이를 파악하면서 나눗셈 활동에 참여할 수 있도록 하였습니다.


아이들이 가장 많이 활용하는 방법(1을 전체로 보는 방법)을 활용하여 함께 정리하였습니다. (나누는 수)로 항상 수가 나뉘게 되니 이는 (분모)가 되고, 이를 분모로 하는 단위분수가 항상 (나누어지는 수)만큼 개수가 있게 됩니다.
따라서 (나누어지는 수)는 분자가 되고, (나누는 수)는 분모가 되니 a ÷ b = a/b가 됨을 확인하였습니다.

3. 탐구 질문 생각하기
아이들과 함께 궁금해했던 질문들에 대해 생각해보는 시간을 가졌습니다. 왜 4학년 때 배운 나눗셈에서는 몫과 나머지를 구하는데 6학년때 배우는 나눗셈에서는 분수로 답을 표현할까요?
아이들에게 두 개의 문제 상황을 제시하면서 오늘 배운 내용과 어떤 점이 다른지 물어보았습니다.
아이들은 이 문제를 해결해보면서 아~라고 바로 이야기하였습니다. 1보다 작은 것으로 표현이 가능한 것은 분수로 표현할 수 있지만 1보다 작은 것으로 표현할 수 없는 것들도 세상에 많이 있기 때문에 이와 같은 경우에는 몫과 나머지로 표현할 수 밖에 없음을 확인하였습니다.

'초등 6학년 수학' 카테고리의 다른 글
| 1. 분수의 나눗셈, (진분수)÷(자연수) 원리 탐구하기2 (0) | 2024.07.03 |
|---|---|
| 1. 분수의 나눗셈, (분수)÷(자연수) 원리 탐구하기 (1) | 2024.06.29 |
| 1. 분수의 나눗셈, 나눗셈(등분제, 포함제) 알아보기 (1) | 2024.06.27 |
| 1. 분수의 나눗셈_분수와 나눗셈에 대한 궁금증으로 탐구 질문 만들기 (0) | 2024.06.26 |
| 2. 각기둥과 각뿔, 단원 성취기준 도달 확인 평가(6학년 1학기) (1) | 2024.06.21 |




