고정 헤더 영역
상세 컨텐츠
본문

지난 시간에는 (진분수)÷(자연수)에 대해 원리 탐구를 해보았습니다. 이번 시간에는 (대분수)÷(자연수)에 대한 원리를 탐구해보는 시간을 가졌습니다.
(진분수)÷(자연수) 원리를 탐구할 때 분자와 자연수가 나누어떨어지는 경우와 나누어떨어지지 않는 경우를 나누어서 원리를 탐구했었는데, (대분수)÷(자연수) 의 경우도 대분수의 자연수 부분과, 분자가 나누는 수의 자연수가 나누어 떨어지는 경우와 나누어떨어지지 않는 경우를 나누어서 원리 탐구를 할 계획입니다.
이번 시간에는 나누어떨어지는 경우에 초점을 맞추어 수업을 진행하였습니다 .
1. (대분수)÷(자연수) 개별 원리 탐구하기
먼저 문제를 제시한 뒤 이번에 배울 식에 대해 함께 살펴보았습니다.

그런 다음 각자 문제 해결할 방법에 대해 생각하며 짝과 함께 어떻게 해결하면 좋을지 이야기를 나누어보았습니다. 그런 다음 아이들은 각자 문제를 나름의 방법으로 해결하였습니다.
2. 분수 그림으로 해결
우리반의 경우 수학 문제를 시각적으로 해결하는 경우를 강조하기 때문에 그림으로 해결하는 아이들이 많습니다. 대분수의 나눗셈의 경우 그림으로 그리더라도 그 해석이 다를 수 있기 때문에 거거에 초점을 맞추어 수업을 하였습니다.

이 아이는 2와 4/5인 대분수를 그림으로 표현할 때 모두 5등분으로 만든다음 다시 ÷2를 하여 10등분으로 만들었습니다. 이 경우는 대분수를 가분수로 바꾸어 문제를 해결한 경우라고 할 수 있습니다.

이 아이는 2와 4/5에서 자연수 부분인 2와 진분수 부분인 4/5를 2등분으로 자르지 않고 2곳으로 나누어 옮겼습니다. 이 경우는 대분수를 가분수로 바꾸지 않고 바로 문제를 해결한 경우라고 할 수 있습니다.
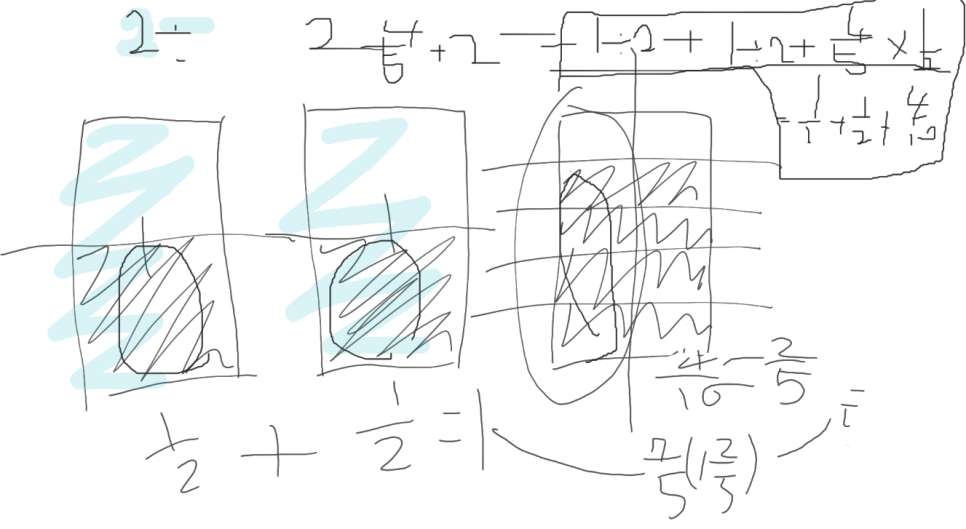
이 경우는 2와 4/5를 각각 1과 1과 4/5로 두고 각각 반으로 잘라 1/2, 1/2, 4/10을 구한뒤 이를 모두 더해 문제를 해결한 학생입니다. 식보다 그림을 먼저 볼 수 있는 아이라고 생각합니다.
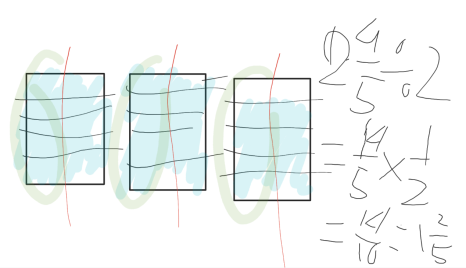
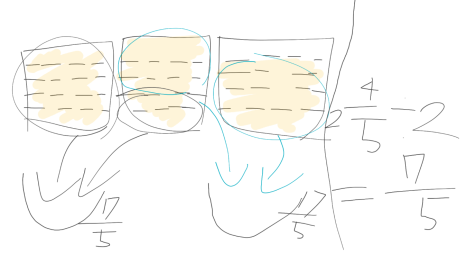
이렇게 아이들마다 다양하게 분수 문제를 해석하며 문제를 풀 수 있어 아이들과 이야기를 나누에 방법들의 공통점과 차이점에 대해 이야기를 나누며 수업을 진행하였습니다.
3. 지난 시간에 알아낸 원리 활용하기(나눗셈의 의미)
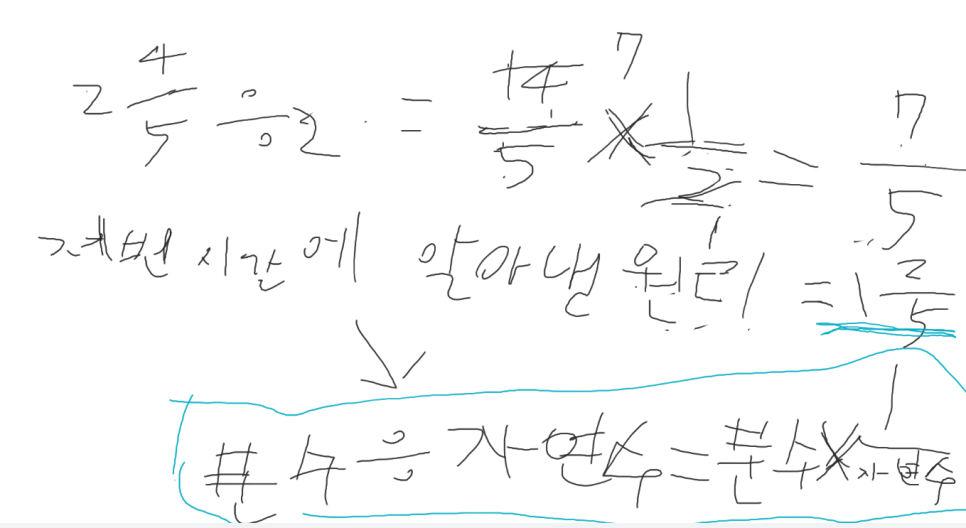
이 아이는 지난시간에 배운 원리를 활용하여 ÷(자연수)는 ×1/(자연수)로 바꿔 해결하였습니다. 나눗셈의 의미가 똑같이 나누었을 때 한 명이 가지는 양을 의미하기 때문에 이는 ×1/(자연수)일 때 분수의 의미가 같이 때문에 바꿔 해결할 수 있음을 약속하여 다음 시간에 그대로 적용하였습니다.
4. 모둠 토의를 통한 (대분수)÷(자연수) 원리 발견하기
모둠별로 토의를 하며 (대분수)÷(자연수)의 원리를 찾아보도록 하였습니다. (진분수)÷(자연수)를 할 때의 원리를 생각하면서 모둠 토의를 한 흔적이 있어 배웠던 내용을 잘 기억하고 있구나 생각이 들었습니다.





사실 이렇게 결과가 나온 이유는 원리를 검증할 때 검증 문제를 다음과 같이 제시하였기 때문이라고 생각합니다. 가분수로 바꾸어서 해결한다는 아이도 처음에는 있었지만 24와 12/17 ÷ 6 의 문제를 해결해 보면서 가분수로 항상 바꾸는 것보다 대분수의 자연수부분과 분자가 나누는 수의 자연수와 나누어떨어진다면 바로 나누는 것이 훨씬 편리하다는 것을 알고 난 뒤 모두 저 원리를 선호하게 되었던 것 같습니다.

5. 학생들 공책 정리




'초등 6학년 수학' 카테고리의 다른 글
| 1. 분수의 나눗셈, 문제 해결하기 (3) | 2024.07.22 |
|---|---|
| 1. 분수의 나눗셈, (대분수)÷(자연수)(2) 원리 탐구하기 (0) | 2024.07.10 |
| 1. 분수의 나눗셈, (진분수)÷(자연수) 원리 탐구하기2 (0) | 2024.07.03 |
| 1. 분수의 나눗셈, (분수)÷(자연수) 원리 탐구하기 (1) | 2024.06.29 |
| 1. 분수의 나눗셈, (자연수)÷(자연수) 원리 탐구하기 (0) | 2024.06.28 |




