고정 헤더 영역
상세 컨텐츠
본문

지난 시간에는 약수가 배수가 무엇인지에 대해 알아보고, 배수의 규칙과 수의 성질에 대해 알아보았습니다. 이번 시간에는 배수와 약수의 관계에 대해 알아보고자 합니다.
1. 약수와 배수의 관계 알아보기
배수와 약수의 관계를 알아보기 위해서는 사실 곱셈과 나눗셈의 관계를 알고 있어야 합니다. 그래서 먼저 정사각형 18개로 만들 수 있는 직사각형을 모두 그려보도록 하였습니다. 대부분의 아이들이 다 그리고 난 다음 만든 직사각형을 식으로 표현해보도록 하였습니다. 그럼 6개의 식으로 표현할 수 있는데 이를 짝에게 약수와 배수를 활용해서 설명해보도록 하였습니다.
식을 대부분 곱셈식으로 표현해서인지 대부분의 아이들이 배수로 설명을 하였습니다. 18은 1의 배수이다. 18은 6의 배수이다. 등으로 표현을 하였습니다. 그래서 약수의 방법으로도 표현해보도록 하고 몇몇 친구들에게 예시를 보이도록 하니 이제 18의 약수는 1, 2, 3, 6, 9, 18임을 이야기하면서 약수의 개념으로 설명을 하였습니다.
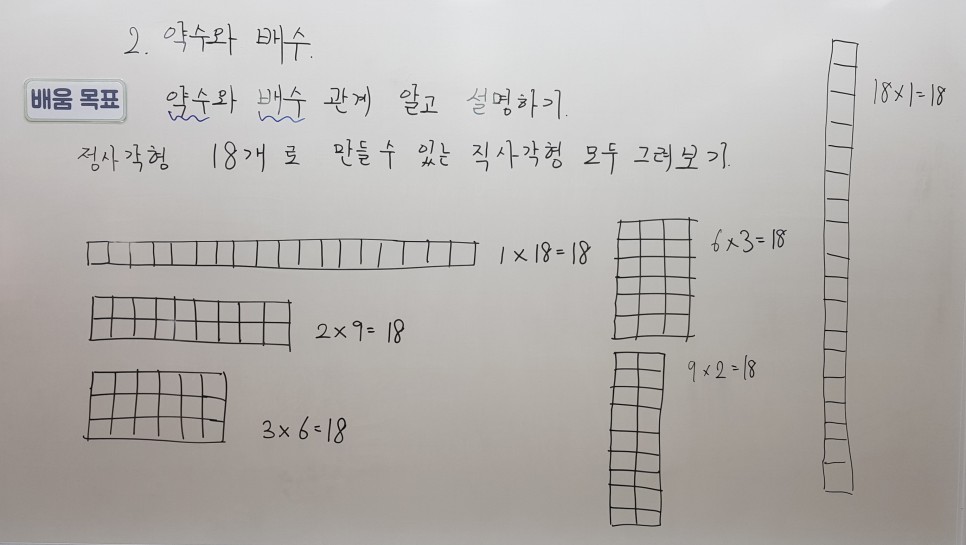
그후 아이들에게 몇 가지 질문을 던져보았습니다.
1, 2, 3, 6, 9, 18은 18의 약수라고 하였는데,
4.5 × 4 = 18이니 4.5나 4도 18의 약수인가요?
아이들은 잠시 고민을 하다가 자연수가 4.5는 자연수가 아니기 때문에 약수가 아니라고 했습니다. 또 약수와 배수는 자연수의 성질이기 때문에 자연수만 해당되고 자연수가 아닌 수가 포함되면 약수가 되지 않는다고 하였습니다.
곱셈식을 통해 약수와 배수 개념을 정리한 다음 짝이 제시하는 곱셈식에 대해 약수나 배수로 서로 이야기 하도록 하였습니다. 친구들이 제시한 곱셈식을 보고 약수와 배수를 말로 잘 표현하였습니다.
짝이 6 × 3 = 18 이라고 곱셈식을 이야기하면
본인은 3은 18의 약수다, 6은 18의 약수다, 18은 3의 배수다, 18은 6의 배수다 등으로 표현하도록 하였습니다.
2. 인수들의 곱으로 수 표현하기

아이들에게 다음 질문에 대해 생각해보도록 하였습니다.
6 × 3 = 18이라는 식을 좀 더 쪼개어 (2 × 3) × 3 = 18로 바꾸어 표현할 수 있는가?
아이들은 바꾸어 표현해도 된다고 이야기하였습니다. 1단원인 자연수의 혼합계산에서 6을 쪼개어 2×3으로 표현할 수 있기 때문에 바꾸어도 괜찮다고 이야기했습니다.
그럼 6×3=18에서 6과 3이 18의 약수인데, (2×3)×3=18에서 (2×3)과 3도 18의 약수가 맞는가?
아이들은 당연히 된다고 이야기하였습니다. 모든 수는 인수들의 곱으로 나타낼 수 있고 이를 소수들의 곱으로 표현할 수 있음을 이해한다면 추후 최대공약수나 최소공배수를 이해에 큰 도움이 되기 때문에 미리 좀 다루었는데 일단 아이들은 잘 대답하였습니다.
대답을 잘했기 때문에 조금 더 나아가 질문을 하였습니다.
8×9=72를 2×2×2×3×3=72이 표현할 수 있나요?
그럼 72의 약수를 구해보세요.
72의 약수는 생략된 ×1을 고려하면 2×2×2×3×3에서 모두 찾을 수 있음을 확인하였습니다. 시간이 조금 부족해서 이 내용에 대한 정확한 이해도를 다 파악하지는 못했지만 그래도 대부분이 어렴풋이 이해하는 모습을 보였습니다.
추후 최대공약수와 최소공배수에서 이해도를 다시 하나 번 확인할 기회가 있을거라 생각하고 수업을 마쳤습니다.
'초등 5학년 수학' 카테고리의 다른 글
| 2. 약수와 배수, 공약수와 최대공약수 공식(5학년 1학기) (74) | 2024.02.16 |
|---|---|
| 2. 약수와 배수, 공약수와 최대공약수 알아보기(5학년 1학기) (62) | 2024.02.15 |
| 2. 약수와 배수, 배수의 규칙 및 수의 성질 알아보기(5학년 1학기) (59) | 2024.02.13 |
| 2. 약수와 배수, 약수와 배수 알아보기(5학년 1학기) (71) | 2024.02.13 |
| 1. 자연수의 혼합계산, 학습지를 통한 실생활 문제해결(5학년 1학기) (69) | 2024.02.12 |




