고정 헤더 영역
상세 컨텐츠
본문


이제 학생들이 다각형의 넓이를 구하는 것에 대해 조금씩 익숙하게 느끼고 있다는 생각이 들었습니다. 넓이를 길이와는 다른 단위로 인식하고, 다각형의 넓이를 구할 때 단위 넓이 몇 개가 포함되는지 알아보아야 하기 때문에 다각형의 모양을 바꿔야 한다는 것과과 모양이 바뀌어도 넓이는 변하지 않는다는 것도 잘 이해하고 있었습니다.
1. 사다리꼴의 넓이 구하는 방법 알아보기
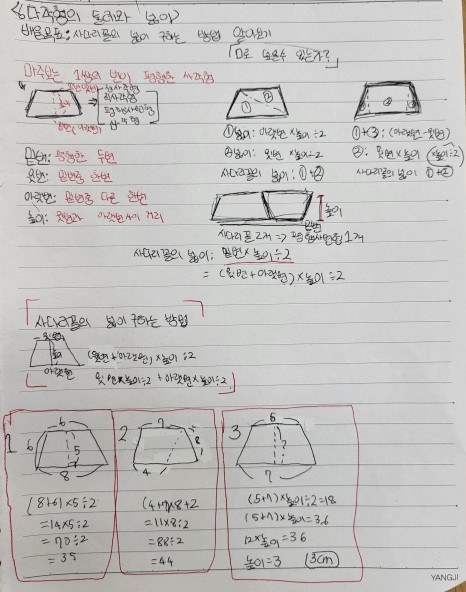
이번 시간에는 사다리꼴의 넓이를 구하는 방법에 대해 알아보았습니다. 먼저 사다리꼴이 무엇인지 다시 한 번 확인하였습니다. 사다리꼴은 마주보는 한 쌍 이상의 변이 평행인 사각형입니다. 이 사다리꼴의 넓이를 구해야 하는데, 사다리꼴을 단위넓이로 덮을 수 있는지 물어보았습니다. 아이들은 덮을 수 없다고 답하였습니다.
그래서 모양을 바꾸어야 하는데, 우리가 넓이를 구할 수 있는 다각형이 이미 정사각형, 직사각형, 평행사변형, 삼각형이 있으니 이 모양으로 변형하면 해결할 수 있음을 확인하였습니다.

오늘은 교과서 부록에 있는 사다리꼴 사진을 활용하여 사다리꼴의 모양을 바꾸어보도록 하였습니다.


먼저 사다리꼴 하나를 사용해서 자르거나 줄을 그어 우리가 넓이를 구할 수 있는 도형의 모양으로 나타낼 수 있도록 하였습니다. 아이들은 2가지 형태로 구했는데, 첫번째는 사다리꼴에 대각선을 그어 두 삼각형으로 나타낸 경우, 두번째는 사다리꼴의 가운데 부분이 직사각형이 되도록 하고 양쪽은 삼각형으로 남긴 경우였습니다.
2. 두 개의 삼각형으로 사다리꼴 넓이 구하기
사다리꼴에서 밑변과 높이, 윗변과 아랫변에 대해 정의했습니다. 마주보는 변을 모두 밑변이라 할 수 있고, 그 중 한 변을 윗변, 나머지 한 변을 아랫변이라고 합니다. 그리고 윗변과 아랫변 사이의 거리를 높이라고 정의하였습니다.
첫번째 경우는 두 개의 삼각형의 넓이를 구해 더하면 사다리꼴의 넓이가 됩니다.
1번 삼각형의 넓이는 (아랫변) × (높이) ÷ 2 이고 2번 삼각형의 넓이는 (윗변) × (높이) ÷ 2 입니다. 1번과 2번 삼각형의 넓이를 더하면 (아랫변) × (높이) ÷ 2 + (윗변) × (높이) ÷ 2입니다.
두번째 경우는 직사각형과 양쪽의 삼각형을 하나로 만든 삼각형의 넓이를 구해 더하면 사다리꼴의 넓이가 됩니다.
직사각형의 넓이는 (윗변) × (높이)이고, 하나로 만든 삼각형의 넓이를 구하면 {(아랫변) - (윗변)} × (높이) ÷ 2입니다. 직사각형과 삼각형의 넓이를 더하면 (아랫변) × (높이) ÷ 2 + (윗변) × (높이) ÷ 2입니다.
즉 사다리꼴의 넓이는 (아랫변) × (높이) ÷ 2 + (윗변) × (높이) ÷ 2이고 좀 더 쉽게 변형하면 {(아랫변)+(윗변) × (높이) ÷ 2임을 확인할 수 있었습니다.
3. 직사각형이나 평행사변형으로 사다리꼴 넓이 구하기
다음은 사다리꼴 2개를 가지고 직사각형이나 평행사변형 등의 모양으로 변형하여 넓이를 구해보도록 하였습니다. 아이들은 하나의 사다리꼴을 뒤집은 뒤 기존의 사다리꼴과 붙여 평행사변형으로 만들어 넓이를 구하였습니다.
평행사변형의 넓이는 (밑변) × (높이)인데, 사다리꼴 2개로 평행사변형 1개를 만들었기 때문에 평행사변형을 2로 나누어야 합니다. 또 평행사변형의 (밑변)은 사다리꼴의 (윗변)과 (아랫변)을 더한 것입니다.
따라서 사다리꼴의 넓이는 {(아랫변)+(윗변) × (높이) ÷ 2임을 알 수 있고 모든 경우 다 동일하다는 것을 확인할 수 있었습니다.
4. 사다리꼴 넓이 구하는 방법 정리하기

사다리꼴의 넓이 구하는 방법을 정리하고, 문제를 3가지 형태로 제시하였습니다. 다들 사다리꼴 넓이 구하는 방법에 따라 잘 해결하는 모습을 보여주었습니다.
세번째 문제를 해결한 친구가 이항 개념으로 문제를 풀었는데, 아이들이 풀이 방법에 대한 질문이 많아서 이항에서 생략된 부분을 간단하게 이야기하고 마쳤습니다. 그래도 아이들이 사각형의 넓이는 어렵지 않게 잘 해결하는 것 같습니다.
5. 학생 공책 정리






'초등 5학년 수학' 카테고리의 다른 글
| 1. 수의 범위와 어림하기, 성취기준 분석 및 궁금증을 통해 탐구질문 만들기(5학년 2학기) (30) | 2024.03.27 |
|---|---|
| 6. 다각형의 둘레와 넓이, 마름모의 넓이 구하는 방법, 원리, 공식 알아보기(5학년 1학기) (3) | 2024.03.26 |
| 6. 다각형의 둘레와 넓이, 삼각형 넓이 구하는 방법(5학년 1학기) (47) | 2024.03.24 |
| 6. 다각형의 둘레와 넓이, 평행사변형 넓이 구하는 방법(5학년 1학기) (52) | 2024.03.23 |
| 6. 다각형의 둘레와 넓이, 표준 단위 넓이 간의 관계, 넓이 감각 익히기(5학년 1학기) (48) | 2024.03.22 |




