고정 헤더 영역
상세 컨텐츠
본문
지난 시간에는 자연수의 혼합계산에서 자연수와 덧셈 및 뺄셈 연산에 대해 이전 학년에도 배웠던 개념과 원리를 정리해 보았습니다. 이번 시간에는 곱셈과 나눗셈 연산에 대해 배웠던 내용을 정리해보고자 합니다.

1. 곱셈 원리 확인하기
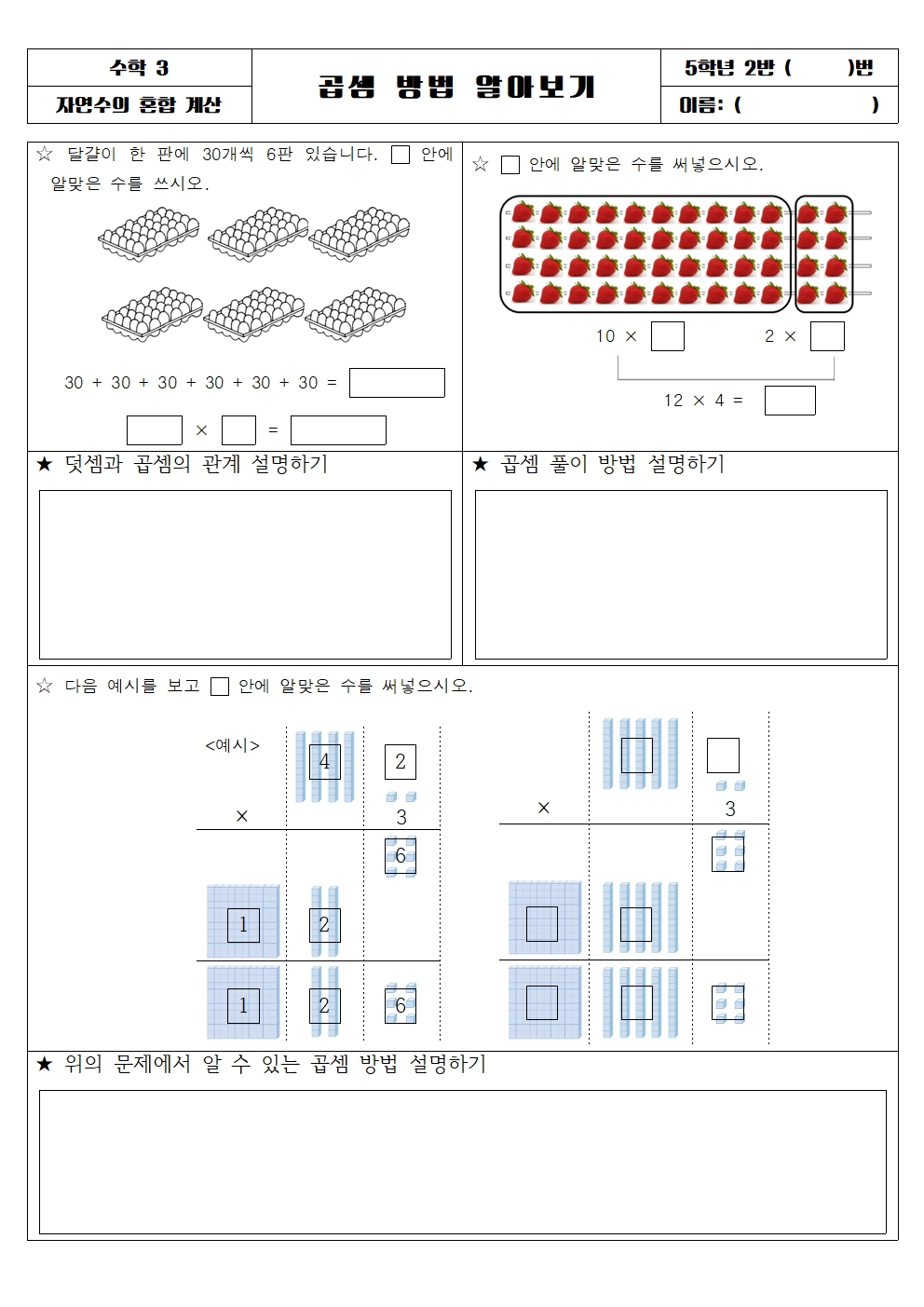
이전에 배웠던 곱셈 원리를 학습지로 확인해보았습니다. 먼저 곱셈을 동수누가로 이해할 수 있는지, 배의 개념으로 이해할 수 있는지 등에 대해 확인하였습니다. 그런 다음 이제 곱셈은 동수누가의 개념보다는 '배의 개념'에 초점을 맞출 수 있도록 강조했습니다.
(곱셈의 결과) = (물건의 개수) × (몇 배)
수학 자체가 구체물을 조작해보면서 수의 개념을 이해하고 이를 그림으로 표현하거나 식으로 표현하도록 발전되는 과정이기에 항상 그림이나 구체물을 통해 수학을 이해하도록 하고 있어요. 그리고 그림과 식을 연관지어 생각할 수 있음을 강조했습니다.
2. 나눗셈 원리 확인하기

나눗셈은 학생들의 오류가 참 많은 곳입니다. 일단 학생들은 3학년 때 나눗셈의 2가지 의미(등분제, 포함제)에 대해 배웠는데 단 한명도 두 가지 의미 차이를 이야기 하지 못했습니다. 그리고 등분제를 그림으로 표현하는 것을 정확하게 하는 학생도 없었습니다.
등분제로 표현해야 할 것을 포함제처럼 묶어서 접시로 옮기는 경우가 많았어요. 그리고 나눗셈과 뺄셈의 관계에서도 똑같은 수를 계속 뺄 때 0이 나오면 나눗셈 식으로 바꿀 수 있고, 몇 번 빼면 0이 되는지 확인하는 그 횟수가 나눗셈의 몫이 됨을 친구가 이야기했음에도 뺄셈 식이 잘못되어 있는 경우가 있었어요.
나눗셈을 확실하게 이해하고 있는 학생이 많지 않음을 알 수 있었습니다. 나눗셈에 대한 지도가 더 필요할 것으로 느껴졌어요.
3. 동수누감
나눗셈의 의미 중 하나가 동수누감입니다. 포함제 개념에 해당하는 것으로 같은 값을 누적해서 뺀다는 의미입니다. 즉 24÷6=이란 24를 6씩 빼면 4번 뺏을 때 0이 됩니다.
24-6-6-6-6=0이 될 때 24를 6씩 4번 빼면 0이 되므로 이는 24÷6=4로 표현할 수 있습니다. 뺄셈에서는 거듭 빼서 0이 될 때까지 빼야하고 이를 나눗셈 식으로 표현하면 몫은 몇 번 뺏을 때 0이 되는지를 확인하면 됩니다.
만약 거듭 빼서 0이 나오지 않는다면 이는 나누어떨어지니 않는 나눗셈이 됩니다.
4. 몫의 의미
몫은 답이다라고 생각하는 학생들이 많이 있어 몫의 의미가 무엇인지에 대해 이야기나누었습니다.
나눗셈에서 몫은 똑같이 나누어서 한 사람이 가져가는 양이 얼마인지 구하는 것
나눗셈 몫의 의미는 위와 같지만 학생들의 대부분은 한 사람이 가져가는 양까지는 생각 못하고 똑같이 나누면 나눗셈이라고 생각하는 경향이 있습니다. 한 사람이 가져가는 양을 몫으로 인식하는데 혼란이 있으면 곱셈에서의 응용 문제나 추후 분수 곱셈 및 나눗셈에서 이해에 어려움이 있을 수 있기 때문에 몫의 의미를 명확하게 인식하도록 하였습니다.
아이들에게 나눗셈 문제를 만들어보도록 하고 아이들이 만든 문제에서 구하는 것이 무엇인지 잘 생각해보도록 한 뒤 몫의 의미를 찾아보도록 하였습니다. 몫의 의미는 사실 등분제에 더 가까움에도 불구하고 포함제로 많이 해결하였습니다. 등분제와 포함제를 그림으로 해결해보면서 몫이 가지는 의미를 명확하게 정리하도록 하였습니다.
5. 정리하기
단원의 초반에 아이들이 어디까지 알고 있는지 확인하고 아이들의 부족한 점을 채울 수 있도록 수업을 준비하였습니다. 다른 연산에 비해 나눗셈의 원리 이해가 부족하여 나눗셈에 대한 공부에 더 많은 시간을 투자하였습니다.
'초등 5학년 수학' 카테고리의 다른 글
| 2. 약수와 배수, 약수와 배수 알아보기(5학년 1학기) (71) | 2024.02.13 |
|---|---|
| 1. 자연수의 혼합계산, 학습지를 통한 실생활 문제해결(5학년 1학기) (69) | 2024.02.12 |
| 1. 자연수의 혼합계산, 왜 곱셈은 덧셈보다 먼저 계산해야 할까요? (63) | 2024.02.10 |
| 1. 자연수의 혼합계산, 덧셈과 뺄셈이 섞여 있는 식 계산하기(5학년 1학기) (70) | 2024.02.09 |
| 1. 자연수의 혼합계산, 자연수와 덧셈 뺄셈 연산(5학년 1학기) (79) | 2024.02.07 |




